La transmission de données

Le problème général est de transmettre à distance une suite de symboles (des zéros et des uns), en empruntant un support quelconque: câble coaxial, paire de cuivre, ondes hertziennes, fibre optique,....  Nous avons vu précédemment le rôle du codage qui était d'adapter le signal au support choisi et de permettre la récupération du rythme.

Dans le cas particulier qui nous intéresse, transmission d'un signal à 2,048 Mbit/s, codé en biphase, sur un support radioélectrique, le signal à émettre se présente comme nous l'avons vu, de la manière suivante:

 

Si la largeur de bande du support était infinie, ou très grande, le signal pourrait sans grand inconvénient être transmis tel quel. Seul le bruit large bande pourrait nous gêner. Cependant, lorsqu'on transmet un signal par radio, on cherche toujours à maîtriser ou à réduire l'encombrement spectral et la bande transmise. On dit alors que le canal est à bande limitée. Il va agir comme un filtre qui va déformer le signal émis.

Quelles sont les déformations que le canal va apporter au signal ?

Tout d'abord, le signal sera reçu avec un certain retard. Ensuite, les fronts de montée et de descente du signal seront bien moins raides. Enfin, et c'est le plus grave, des suroscillations encadreront le signal utile. L'importance de ces phénomènes dépend étroitement des caractéristiques du canal: bande passante et courbe de réponse du filtre.

Comme les symboles transmis s'enchaînent rapidement, les suroscillations correspondant à un symbole reçu perturberont la réception des symboles suivants. On dit que l'on observe des interférences intersymboles.

L'échantillonnage

 

Le signal reçu a une nature analogique. Le problème que l'on a à résoudre à la réception est de transformer le signal reçu en un signal le plus conforme possible au signal numérique émis, c'est à dire avec le moins d'erreurs possibles.

Pour cela on décidera à intervalles réguliers, si le symbole transmis est un "0" ou un "1", en comparant la valeur du signal reçu à un seuil fixé. Par exemple, si à l'instant choisi le signal reçu est supérieur à une certaine valeur on décidera que l'on a reçu un "1", dans le cas contraire un "0". Bien évidemment, l'opération doit s'effectuer au rythme de  la transmission, très précisément.

instants d'échantillonnage:

A l'instant d'échantillonnage, la décision sera prise en fonction en fonction de la valeur instantanée du signal reçu, qui est lui-même la composition du signal utile, du bruit et de l'interférence intersymbole. On a bien évidemment intérêt à minimiser cette dernière.

Comment annihiler l'effet de l'interférence intersymboles ?

C'est très simple! Il suffit de choisir astucieusement le filtrage apporté par le canal pour que les suroscillations parasites passent par zéro au moment précis où l'on effectuera l'échantillonnage.

Les filtres de Nyquist possèdent cette propriété.

Pour en savoir plus: les aspects théoriques, par Jean-Claude Imbeaux, F6AXK
        Merci pour cette contribution, précieuse pour la réalisation de notre filtre.

La réalisation de notre filtre de Nyquist

La synthèse du filtre

On supposera que le filtrage du canal est donné pour l'essentiel par les filtres que nous insèrerons. Les opérations de préaccentuation/désaccentuation CCIR 405-1, qui sont effectuées pour conserver une compatibilité totale avec les signaux ATV analogiques, ont pour effet de "colorer" le bruit et de rendre difficile l'étude d'optimisation de la répartition du filtrage de Nyquist entre émission et réception. Dans une première approche expérimentale nous partagerons de manière équilibrée le filtrage entre émission et réception.

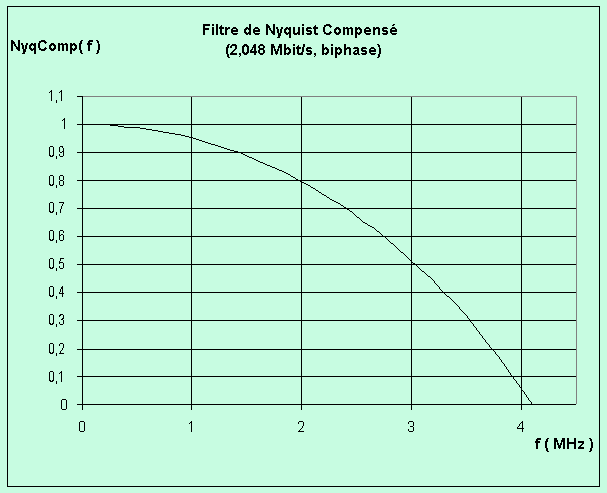
En prenant f égal à 2,048 MHz et un roll-off de 1 dans les calculs présentés ci-dessus, on obtient la réponse souhaitée du filtrage global:

Comme pour une étude précédente sur la préaccentuation TV, des simulations peuvent se réaliser très simplement au moyen d'un logiciel Spice. Il en existe de nombreuses versions gratuites ou commerciales.
Pour un usage amateur, on pourra télécharger le logiciel gratuit Spice Opus sur http://fides.fe.uni-lj.si/spice/, puis un petit document explicatif de 5 pages sur http://fides.fe.uni-lj.si/spice/getstarted/getstarted.html. Le site, très sympathique, fournit également de nombreux exemples d'utilisation. Au bout d'une heure de prise en main, on en sait assez pour se lancer dans des simulations.

Le filtre à réaliser doit possèder un comportement de type passe-bas.   L'impédance caractéristique sera choisie égale à 300 ohms pour que le filtre puisse être attaqué directement à partir de circuits logiques.... En disposant deux cellules de filtrage en pi en cascade et rendues "molles", c'est à dire amorties, nous avons pu obtenir exactement la forme requise, juqu'à une fréquence de 3,5 MHz. Malheureusement, la distorsion de temps de propagation de groupe était excessive (près de 100 ns), ce qui conduisait à une déformation sensible du signal.

En effet, un filtre idéal introduit un retard pur et uniforme. Dans un filtre réel, le retard apporté dépend souvent de la fréquence, et ça, ça peut ne pas être bon du tout ! Si les fréquences hautes ne se propagent pas à la même vitesse que les fréquences basses, le signal transmis peut se retrouver passablement déformé. On estime généralement que la variation du retard dans la bande de fréquence à transmettre doit être inférieure à 20% de la durée du symbole. Dans notre cas particulier où la rapidité de modulation du signal biphase est de 4 MBauds, la durée du symbole élémentaire est de 250 ns, et la distorsion de temps de propagation de groupe doit être inférieure à 50 ns.

Après quelques tâtonnements en simulation on obtient un résultat pas trop différent de celui escompté, avec une cellule en pi simple, corrigée par le dipôle R1 L2.

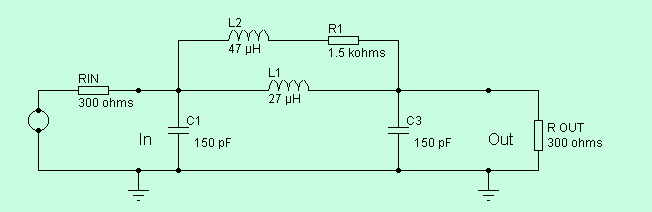
A gauche, la source, avec sa résistance interne de 300 ohms. A droite, l'utilisation dont la résistance interne doit être également de 300 ohms.

La "netlist" Spice peut s'écrire :

Nyquist filter, group delay
* nyquist.cir file
.control
ac lin 101 45KHz 4.5Meghz
let phase = vp(4) + 2*pi*(vp(4) lt 0) - 2*pi
plot phase
GD = -1e9*2*(phase[1,100] - phase[0,99])/(45000*2*pi)
plot GD xlabel f[Hz] ylabel group_delay[ns]
unlet phase
plot 4*(vm(4)^2) xlabel f[Hz] ylabel response ylimit 0 1.1
.endc
* voltage resources
v1 1 0 dc 0V ac 1 sin 0 1V 10megHz
* resistors
ri 1 2 300
ro 4 0 300
R1 2 5 1500
* capacitors
C1 2 0 150pF
C2 4 0 150pF
* inductances
L1 2 4 27uH
L2 5 4 47uH
.end

On sauvegarde la netlist sous le nom de fichier "nyquist.cir". En lançant ensuite Spice Opus avec la commande "source nyquist.cir" on obtient, pour deux filtres en cascade (le Nyquist émission + le Nyquist réception) la courbe de réponse suivante:

 

 

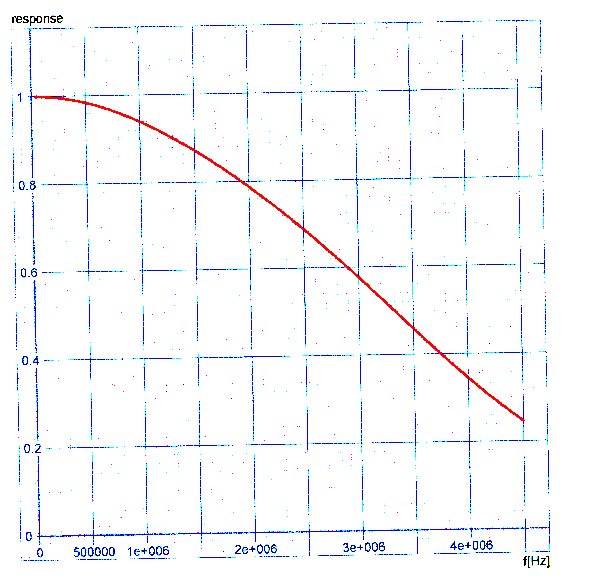
Et la courbe de temps de propagation de groupe suivante:

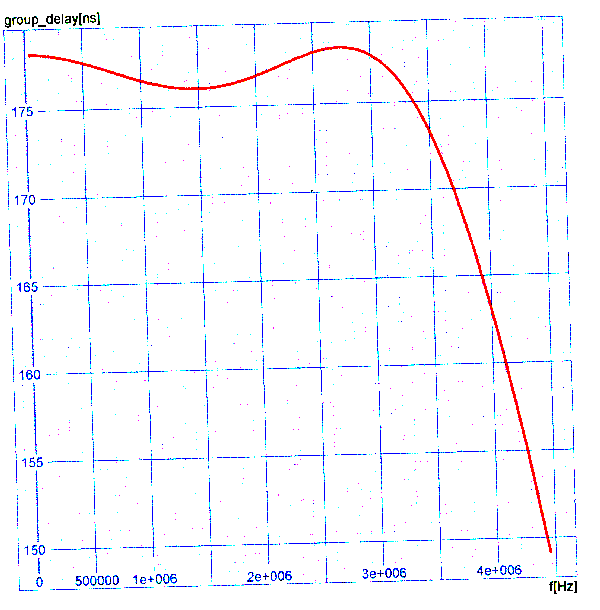
Le retard moyen apporté par les deux filtres (émission + réception) est compris entre 173 ns et 178 ns. Le temps de propagation de groupe est constant à 4 ns près dans la bande 0,5 MHz à 3,5 MHz, ce qui est excellent.

Les déformations du signal (cf diagramme de l'oeil) sont vraisemblablement dues aux écarts de la réponse en amplitude par rapport à la courbe théorique . Pour notre application, nous souhaitons une structure de filtre simple. Nous en resterons donc là pour l'instant, en réservant pour plus tard une meilleure optimisation globale du filtrage de Nyquist, en particulier par la mise en cascade de deux cellules corrigées, analogues à celle décrite ci-dessus.

 

Pour résumer cette page:

Lorsqu'on désire transmettre des données à haute vitesse, il faut s'efforcer de maîtriser les courbes de réponse amplitude-fréquence et phase-fréquence du canal de transmission. Ca ne fait pas de mal en télévision non plus :-). En transmission numérique, le filtre de Nyquist sert à annihiler l'interférence intersymbole.

Pour une transmission numérique à 2 Mbit/s, codée en biphase, le schéma pratique final du filtre à insérer, une fois dans la chaîne vidéo émission, une autre fois dans la chaîne vidéo réception est le suivant:

La source et l'utilisation doivent présenter une impédance de 300 ohms.