|
Aspects théoriques
du filtrage pour transmission numérique
application à la transmission
en biphase FM
par Jean-Claude Imbeaux,
F6AXK
Filtrage de Nyquist
Le filtrage de Nyquist est destiné à éliminer l’interférence
entre symboles, ce qui permet une décision simple, symbole par
symbole.
Pour un échantillonnage aux instants kT, le critère
de Nyquist dans le domaine temporel est nyq(kT) = 0 , sauf pour
k=0.
Ceci se traduit par une symétrie de la réponse
en fréquence Nyq(f) autour du point de fréquence f=1/2T.
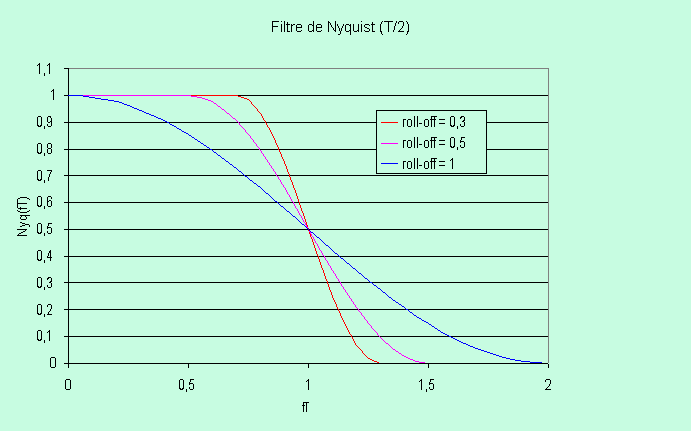
Pour la transmission biphase, on cherche à annuler
la réponse impulsionnelle tous les kT/2, soit nyq(kT/2)=0. La
symétrie de Nyq(f) est alors autour du point de fréquence 1/T.
A l’émission on part d’une forme d’impulsion
rectangulaire de durée T/2, qui doit être prise en compte dans
la réponse globale de la chaîne de transmission.
La combinaison du filtrage émission et du filtrage
réception doit être équivalente à un filtrage de Nyquist compensé,
soit :
NyqComp(f) = Nyq(f) / (sin(p
*fT/2)/(p *fT/2))
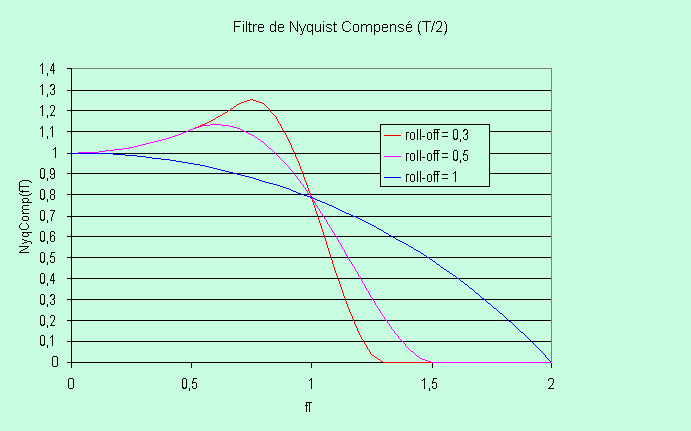
Partage du filtrage
entre émission et réception
Pour une chaîne de transmission linéaire, avec
bruit blanc, le filtrage qui permet de minimiser l’énergie
à transmettre sur le canal, pour un rapport signal à bruit (ou
un taux d’erreur) fixé après filtrage réception, est tel
que :
He(f) = Hc(f)1/2 / g
(f)¼ et Hr(f) = Hc(f)1/2 * g
(f)¼
avec Hc(f) = He(f) * Hr(f) ; combinaison des
filtrages émission et réception
g (f) = densité spectrale
de puissance du signal avant filtrage émission
Pour une transmission numérique classique, avec
des impulsions rectangulaires indépendantes de durée T, et critère
de Nyquist, ceci conduit à :
He(f) = Nyq(f)1/2/ (sin(p
*fT)/(p *fT)) et Hr(f) = Nyq(f)1/2
Le filtrage de Nyquist est partagé entre émission
et réception. De plus le filtrage émission est compensé pour
tenir compte de l’impulsion rectangulaire initiale.
Pour une transmission en biphase, il n’est
pas possible de satisfaire le partage optimal du filtrage, car
le spectre g (f) est nul pour f=0.
L’avantage d’avoir une composante continue nulle se
traduit donc par une dégradation des performances par rapport
au cas classique.
Il est possible de comparer théoriquement trois
cas particuliers :
a) filtrage global (Nyquist Compensé) partagé
de façon identique entre émission et réception, soit :
He(f) = Hr(f) = NyqComp(f)1/2 = ( Nyq(f)/(sin(p
*fT/2)/(p *fT/2)) )1/2
b) filtrage de Nyquist partagé, mais compensation
entièrement à l’émission, soit :
He(f) = Nyq(f)1/2 / (sin(p
*fT/2)/(p *fT/2)) et Hr(f) = Nyq(f)1/2
c) filtrage de Nyquist partagé, mais compensation
entièrement à la réception, soit :
He(f) = Nyq(f)1/2 et Hr(f) = Nyq(f)1/2
/ (sin(p *fT/2)/(p
*fT/2))
Le calcul montre que le cas a) est le meilleur
des trois, mais la différence est très faible (0,3 dB mieux
que le cas b) qui est le plus mauvais).
Transmission biphase
/ FM
La transmission en FM avec préaccentuation et désaccentuation
du signal biphase complique encore la situation, pour deux raisons :
- la chaîne de transmission n’est pas
linéaire (modulation FM)
- le bruit n’est pas blanc après désaccentuation
Le premier point fait qu’il devient impossible
de définir par calcul théorique, le partage optimal du filtrage
entre émission et réception (le second point, sur le bruit non
blanc, peut être pris en compte théoriquement).
La seule connaissance est celle du filtrage global
NyqComp(f) ; cf. §1.
Ensuite, pour aller plus loin, il faudrait avoir
recours à des logiciels de simulations, en incluant la modulation-démodulation
FM.
|